Tesseract, explained.

Gulan Twentyeight

You can try out the demo and come back here or there's a link at the end too.

The formal definition of a tesseract is that it is the four-dimensional analogue of the cube, which is vague on many levels. For starters, the fourth dimension itself is very hard to visualize!

⊕
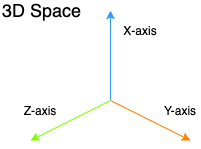
3D space with X, Y and Z axes Consider our normal 3D space, with X, Y and Z axes. Can you imagine another axis perpendicular to all of them? If you take my word for it and believe that such an axis exists (let's call it W), what are the possibilities? Can you have shapes in it? Cylinders, Pyramids, Cubes?

Let's dial it down a notch and go to 0-Dimensional space. There are no X, Y and Z and the only thing that can exist in that dimension is a point. Let's introduce a dimension (say X) and have the point travel on it. If we trace out the path travelled by the point, we get the Line. Technically it's a line-segment.

Now we take the line and add another dimension (Y) and have the line travel down the Y-axis for the same distance. If we trace out that path, we get the Square. If we take the square and then do this same exercise on the Z-axis, we get the Cube.

For the finale, we take the cube and add a fourth dimension (W) and have it move in that dimension. The shape we get is called a Hypercube or a tesseract.

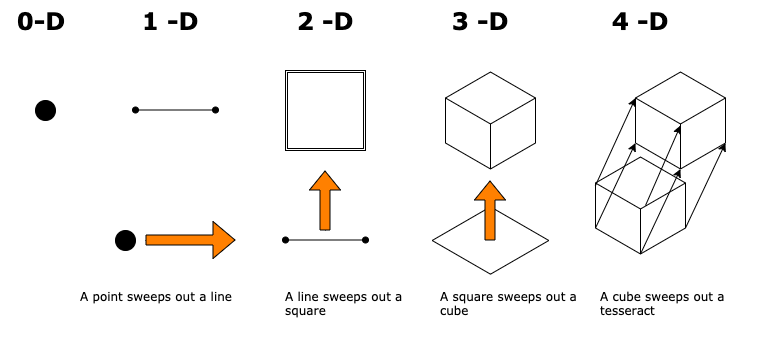
We can have other shapes in four dimensions as well. In fact, we can perform this exercise with other platonic solids and get different shapes. Generally, these shapes are called polytopes. We can say the tesseract is one of the regular 4-polytopes.

⊕
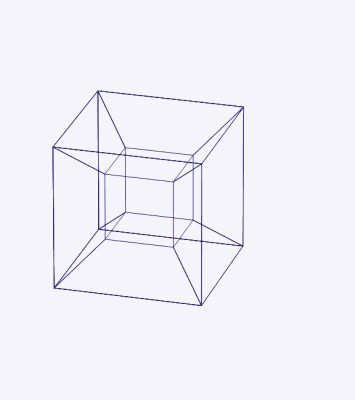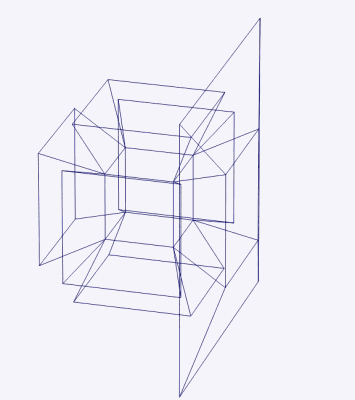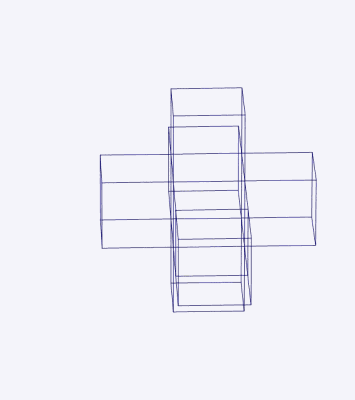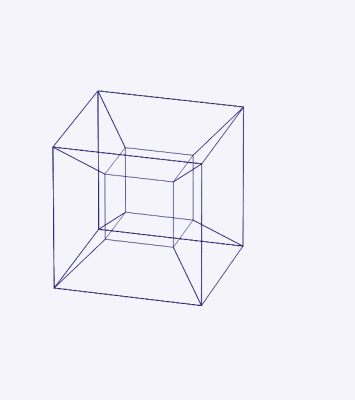
Net of a tesseract.
credits Wikipedia Just as a square is made up of 4 lines and a cube is made up of 6 squares, A tesseract is made up of 8 cubes. Suppose you have a cubical box and you open it up. You get a 2D shape of squares that can be joined up to form the cube again. This opened up figure is called the net of the cube. A particular net of a tesseract looks like a three-dimensional cross and is known as a Dalí cross owing to Salvador Dalí's painting Corpus Hypercubus.

Projection

Now that you have a vague idea about what a tesseract is, let's see how we could visualize one. If you take a cube face a wall and shine a torch on one end, the shadow on the wall would correspond to a square. If you rotate the cube, the shadow also stretches, skews and rotates.

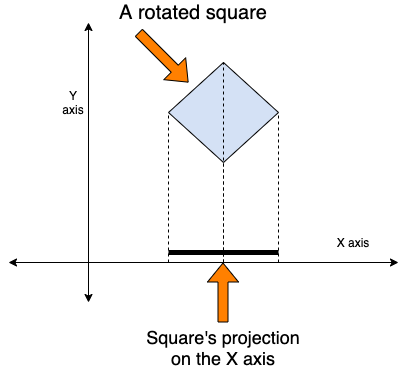
Mathematically this process is called a projection and this underpins all of 3D graphics. That first-person shooter game that you're playing uses projection to show you the 3D world of the game onto your 2D screen. Here's an example of projecting a 2D square on to the X-axis.

You can do this in four dimensional space too. You can project a 4D point onto 3D and if you want, to lower dimensions. You can rotate the tesseract in 4D space and watch the shadow in 3D. Which brings us to...

The Demo

The demo shows you the projection of a tesseract in 3D space. The rotation tab on the upper right corner lets you rotate the tesseract along the XW, YW and ZW planes and moving with the mouse lets you see the rotated shape from different angles.

Since we can't really represent the fourth dimension well, rotating along the W-axis would look like the tesseract is opening up and closing down on itself. The blue part is one of the eight squares that make up the tesseract so that you can get a feel for its position.

Now go play around with it and see if you can visualize how a tesseract would look in four dimensions.

Resources

These are some resources I found useful while building the demo.

The first is this link from the mathematics department at Union college which has detailed explanations about tesseracts, along with some cool animations and videos. It is great for building an intuition so I suggest you check it out.

This video from LeiosOS helped me to understand the rotation and projection matrices needed to display the tesseract.

This observable from Torben Jansen was my definitive resource in grokking three.js and tesseracts. He's used a cool trick with hamming distances to determine the positions of each of vertices of the tesseract. Take a look at it.